调度:PELT算法
PELT全称是per-entity load tracking,翻译过来是一种针对entity的负载追踪技术,这里entity是指内核调度模块内的struct sched_entity,也就是调度单元的基本抽象。而所谓负载追踪,其本质是提供一种衡量负载的指标以及在运行过程中动态计算该指标的方法。
那么,何谓负载?
负载建模
假设系统已运行了$T$时间,而在这段时间内存在某个任务,其运行时间为$\Delta t$,此时我们可以很容易算出该任务的运行占比:
$$
L = \frac{\Delta t}{T} \tag{1}
$$
可以认为,运行占比在某种意义上就是一种负载表现。但公式(1)本身仍存在一些问题,即无法表达时间尺度上不同任务对算力的渴求程度。
举个例子:假设系统中存在有两个任务A和B,其中任务A在过去[0, 1]小时的区间内满转运行,但在截止到当前时刻2的[1, 2]区间内是空闲的;而任务B则相反,在[0, 1]区间空闲,在[1, 2]区间满转。这种场景下我们是不是有理由相信任务B在未来的时间内有更大的概率还是满转的,在只有1个CPU资源可用的情况下应该优先满足任务B?但很不幸的是,这种场景套用上述负载公式将获得两个相同的结果:$1/2 = 0.5$。这说明公式存在时间尺度上的缺陷,无法预测二者在未来的运行情况。因此,需对公式做进一步改造。
具体做法为:
第一步,将时间等分为多个周期,每个周期内的运行占比单独计算(假设当前时刻是$n$):
$$
L = \frac{\Delta t}{T} = \frac{\Delta t_1}{T_1} + \frac{\Delta t_2}{T_2} + … + \frac{\Delta t_{n-1}}{T_{n-1}} + \frac{\Delta t_n}{T_n} \tag{2}
$$
因为周期是等分的,所以公式(2)中分母$T_1 = T_2 = … == T$
第二步,为不同周期赋予不同的衰减系数,其目的是为了让早期的运行占比对整体负载贡献低一些,而让近期的运行占比对整体负载贡献高些。这类需求适合使用等比数列性质的衰减系数:
$$
L = \frac{\Delta t_1}{T_1}y^{n-1} + \frac{\Delta t_2}{T_2}y^{n - 2} + … + \frac{\Delta t_{n-1}}{T_{n-1}}y^{1} + \frac{\Delta t_n}{T_n} \tag{3}
$$
其中,衰减系数$y \in (0, 1)$。
之所以选等比数列,是因为其可以很容易转换为如下递推公式,只需记录上一时刻的值,从而减少内存占用:
$$
L_n = L_{n - 1}y + \frac{\Delta t_n}{T_n} \tag{4}
$$
PELT算法内的负载计算公式即为如此。
计算技巧
接下来就是一些细节问题了:
- 周期$T$取多大合适?
- 衰减系数$y$取多大合适?
- $\frac{\Delta t_n}{T_n}$的值如何计算?
- 因为系数$y$的取值范围在(0, 1)区间内,那么计算过程就涉及到了浮点,浮点计算是耗时的,应如何加速?
问题1/2:T和y取多大合适?
周期T和衰减系数y的取值可能有一些经验成分在里面,内核给出的答案是:$T = 1024us$(近似为1ms),而衰减系数取$y^{32} == 0.5$,表示在过去的第32个周期希望其负载贡献度衰减一半。注意这里的1024和0.5的取值均有讲究,其目的是为了后续的计算可转换为移位的方式,比如对1024做除法,等价于右移10位;而对0.5做乘法,等价于右移1位。
问题3:$\frac{\Delta t_n}{T_n}$的值如何计算?
$\frac{\Delta t_n}{T_n}$为最近的一个周期内的运行占比。其中,分子部分任务的运行时间$\Delta t_n$好统计,分母部分$T_n$等于$T$,也就是1024us。看起来$\frac{\Delta t_n}{T_n}$的值很容易计算,但这是建立在通过定时器周期性观测计算的假设上。内核调度中没有这么做,而是提供了一种支持任意时刻观测计算的方式。显然,这种方式要面对一个棘手的问题:当观测的时刻距离上一计算时刻的时长不满足周期的整数倍时该如何计算。如果能小心处理好该问题,对于调度来讲是大有好处的,即计算负载的自由度更强,且更精确,毕竟任务的存活时间不会完全遵循整数倍的周期。
那么,具体要怎么做?
仍然是按周期分段的思路,即:将[上一计算时刻,这一时刻]这段区间的时间按周期为单位分段细化,并套用衰减公式计算。
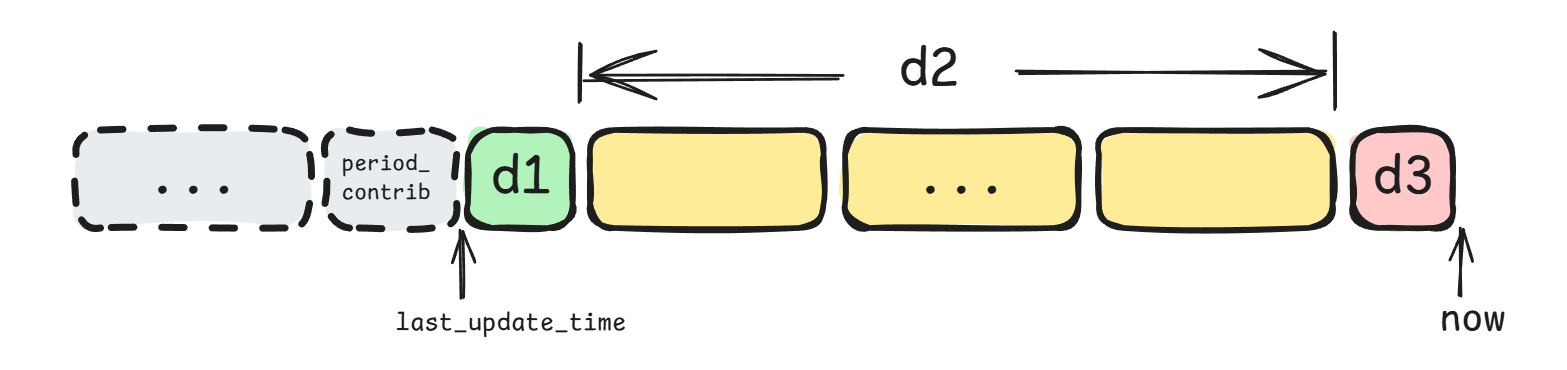
假设上一时刻为last_update_time,上一时刻的负载为$L_{n - 1}$,当前时刻为now,固定周期为1024us,基于此可算出:
[last_update_time, now]这段区间的周期数,记为$p$[last_update_time, 上一时刻的周期结束时间]这段区间的运行时长,记为$d_1$[上一时刻的周期结束时间,当前时刻的周期起始时间]这段区间的运行时长,记为$d_2$[当前时刻的周期起始时间,now]这段区间的运行时长,记为$d_3$
则$\frac{\Delta t_n}{T_n}$可推导如下:
$$
\frac{\Delta t_n}{T_n}
= \frac{d_1 y^p + 1024\sum_{i=1}^{p-1}y^i + d_3y^0}{1024\sum_{i=1}^{+\infty}y^i + d_3} \tag{5}
$$
将该结果代入前面的递推公式(4),即可得到当前时刻now的负载:
$$
\begin{split}
L_n &= L_{n - 1}y’ + \frac{d_1 y^p + 1024\sum_{i=1}^{p-1}y^i + d_3y^0}{1024\sum_{i=1}^{+\infty}y^i + d_3} \\
&= L_{n - 1}y^p + \frac{d_1 y^p + 1024\sum_{i=1}^{p-1}y^i + d_3y^0}{1024\sum_{i=1}^{+\infty}y^i + d_3} \\
&= \frac{uy^p}{1024\sum_{i=1}^{+\infty}y^i + d_1} + \frac{d_1 y^p + 1024\sum_{i=1}^{p-1}y^i + d_3}{1024\sum_{i=1}^{+\infty}y^i + d_3}
\end{split} \tag{6}
$$
其中:
- $y’ = y^p$,因为原本的递推公式只表达1个周期的递推,而这里递推了$p$个周期;
- $u$表示上一时刻的运行时间加权平均结果。
公式(6)中,分子$1024\sum_{i=1}^{p-1}y^i$和分母$1024\sum_{i=1}^{+\infty} y^i$可应用等比数列求和公式来算。
已知等比数列求和公式为:
$$
\sum_{i=0}^{+\infty}y^i = \frac{1}{1-y} \tag{7}
$$
$$
\sum_{i=n}^{+\infty}y^i = \frac{y^n}{1-y} \tag{8}
$$
则分子中的求和可简化为:
$$
1024\sum_{i=1}^{p-1}y^i = 1024(\sum_{i=0}^{p-1}y^i - y^0) = 1024(\sum_{i=0}^{+\infty}y^i - \sum_{i=p}^{+\infty}y^i - 1) = \frac{1024}{1-y} - \frac{1024y^p}{1 - y} - 1024 \tag{9}
$$
分母中的求和可简化为:
$$
1024\sum_{i = 1}^{+\infty}y^i = 1024(\sum_{i = 0}^{+\infty}y^i - y^0) = \frac{1024}{1-y} - 1024 \tag{10}
$$
已知$y^{32} == 0.5$,故可以提前算出$1024/(1-y)$的值,该值在内核中使用了宏LOAD_AVG_MAX来定义。为了公式简洁起见,笔者将其记为常数$b$。
将上述公式(9)和(10)代回到前面的负载公式(6),可得:
$$
\begin{split}
L_n &= \frac{uy^p}{1024\sum_{i=1}^{+\infty}y^i + d_1} + \frac{d_1 y^p + 1024\sum_{i=1}^{p-1}y^i + d_3}{1024\sum_{i=1}^{+\infty}y^i + d_3} \\
&= \frac{uy^p}{b - 1024 + d_1} + \frac{d_1 y^p + (b - by^p - 1024) + d_3}{b - 1024 + d_3}
\end{split} \tag{11}
$$
有没有发现计算量少了许多?
公式(11)的内核实现可以看如下函数:
1、分子计算:__accumulate_pelt_segments()
1 | // file: kernel/sched/pelt.c |
2、分母计算:get_pelt_divider()
1 | // file: kernel/sched/pelt.h |
可以看到,代码和公式(11)基本吻合。
现在的负载公式里就仅剩$val\times y^p$较为复杂,并且y是浮点,这也是前面提到的问题4要解决的,即如何为浮点运算加速。
问题4:浮点运算如何加速?
内核中规避浮点运算的方式是先对原始值放大为整型,和其他值算完后,再右移缩放回去。对于$val\times y^p$,可以这么做:
$$
val\times y^p = val \times (y^p \times 2^{32} >> 32) \tag{12}
$$
我们希望$y^p\times 2^{32}$能够提前计算固化到数组中,便于后续直接查询,为此需想办法将$p$缩小到有限区间内。已知$y^{32} = 0.5$,因此p取值可以通过如下递推限制到[0, 31]:
$$
y^p\times 2^{32} = y^{32}\times y^{p’ - 32} \times 2^{32} = (y^{32})^2\times y^{p’’-32\times 2}\times 2^{32} = … \tag{13}
$$
基于此规律可总结出如下公式:
$$
(y^{32})^{p/32}\times y^{p \mod 32} \times 2^{32} = (0.5)^{p/32}\times y^{p \mod 32}\times 2^{32} \tag{14}
$$
其中:$y^{p \mod 32}\times 2^{32}$可提前计算并使用长度为32的数组容纳,内核中将其定义为runnable_avg_yN_inv;而$(0.5)^{p/32}$,仔细想想它不就是右移运算吗?
公式(14)的内核实现可以查看函数:decay_load()
1 | // file: kernel/sched/pelt.c |




